Dentro de las matemáticas existe un numero mágico llamado PHI. Una descripcion de las interesantes propiedades de este numero se sale de los propósitos de este articulo. Para los interesados, una busqueda en la web de los terminos PHI NUMBER y FIBONACCI NUMBERS, les dará una idea.
El proposito de esta entrada es demostrar de una manera cruda y poco elegante que algunas de las dimensiones de la estrella de 5 picos contiene la propiedad PHI.
Para empezar veamos que es PHI. Digamos que se tiene un segmento de recta AC y este segmento esta compuesto por los segmentos AB y BC. La siguiente figura ilustra esta situación:
La razon PHI se presesnta cuando se cumple la siguiente condición:
Si uno se toma el trabajo de resolver la anterior formula se encontrará que PHI viene dado de la siguiente manera:
Una vez que sabemos que es PHI pasaremos a la demostración que nos ocupa:
Si denotamos por minusculas los angulos opuestos a los segmentos de recta mostrados en la figura anterior; por geometria es posible deducir lo siguiente:
a=72 grados
b=36 grados
Estos son angulos especiales de los cuales se sabe lo siguiente:
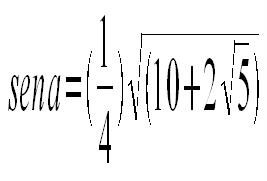
Por identidades trigonometricas se sabe que:
Re-arreglando y sustituyendo tenemos que:
Lo cual demuestra que PHI es igual a la proporcion que hay entre A y B en la estrella de 5 picos.




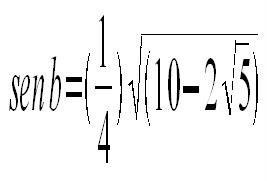


4 comentarios:
esto es una prueba
Hmm didn't know about the credit card thing .. had to measure the dimensions ! Good one
Cool :)
*bookmark*
No comprendo nada
Publicar un comentario